Pentakis dodecahedron
Basic Geometry
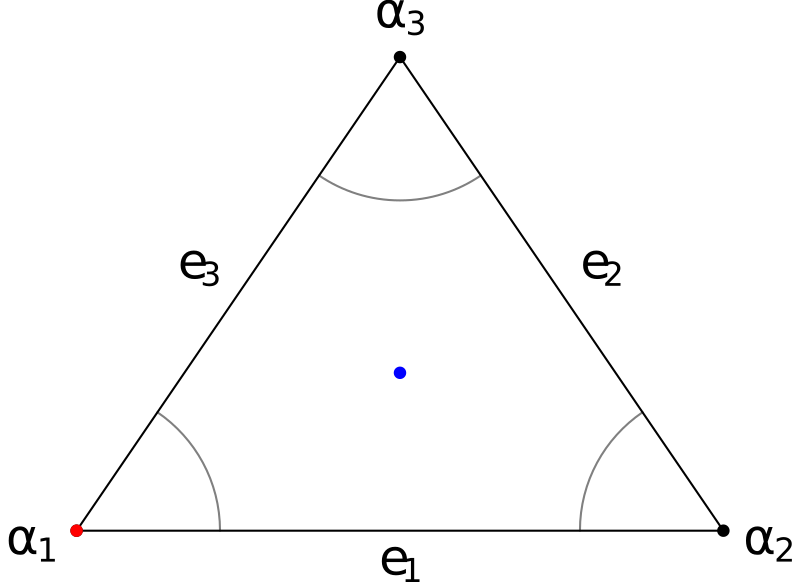
The 3 edge lengths are:
- e1 : $ \frac{38}{3 \sqrt{5} + 27} $ ≈ 1.127
- e2 : $ 1 $ ≈ 1.000
- e3 : $ 1 $ ≈ 1.000
The 3 angles are:
- α1 : $ \arccos{\left (\frac{19}{3 \sqrt{5} + 27} \right )} $ ≈ 55.6906°
- α2 : $ \arccos{\left (\frac{19}{3 \sqrt{5} + 27} \right )} $ ≈ 55.6906°
- α3 : $ - 2 \arccos{\left (\frac{19}{3 \sqrt{5} + 27} \right )} + \pi $ ≈ 68.6187°
Further Properties
Dihedral angles:
- Minimal concave angle: 38.0000°
- Minimal convex angle: 38.0000°
Reversed edges: None
3D View
Show model in 3D viewer.
Similar Shapes
Model Files
Available gap values:- 0.2mm: pentakis-dodecahedron-normal.stl
- 0.25mm: pentakis-dodecahedron-normal.stl
- 0.4mm: pentakis-dodecahedron-normal.stl
To download all files in one big package, see the download page.